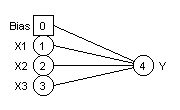
MODELE LINEAIRE

Toute étude statistique commence par un modèle linéaire, ici :
Y = a₀ + a₁X₁ + a₂X₂ + a₃X₃ 
En langage neuronal, les variables X₁, X₂, X₃ sont les neurones d'entrée, la variable Y est le neurone de sortie, les coefficients a₀, a₁, a₂, a₃ sont les valeurs des synapses ajustées au cours de l'apprentissage.

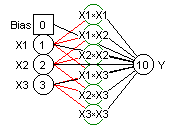
MODELE POLYNOMIAL D'ORDRE 2

Le modèle polynomial d'ordre 2 permet de caractériser l'influence des carrés et des produits croisés, ici :
Y = a₀ + a₁X₁ + a₂X₂ + a₃X₃ + a₄X₁² + a₅X₁X₂ + a₆X₂ ² + a₇X₁X₃ + a₈X₂X₃ + a₉X₃² 
C'est un modèle non-linéaire par rapport aux variables d'entrée mais linéaire par rapport aux coefficients. La solution unique à ce modèle à 10 coefficients requiert au minimum 10 exemples dans la base d'apprentissage.

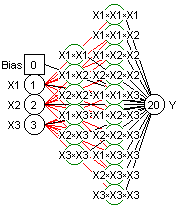
MODELE POLYNOMIAL D'ORDRE 3

Le modèle polynomial d'ordre 3 ajoute une complexité supplémentaire mais reste un modèle linéaire par rapport aux coefficients. Ici, la solution unique à ce modèle à 20 coefficients requiert au minimum 20 exemples dans la base d'apprentissage.

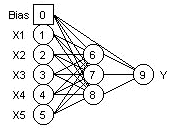
RESEAUX STATIQUES

Les réseaux statiques sont les plus courants parmi les réseaux de neurones. Ce sont des modèles non-linéaires par rapport aux entrées et par rapport aux coefficients car les neurones de la couche cachée, ici les neurones 6, 7 et 8, portent une fonction d'activation non-linéaire de type sigmoïde. Ils sont utilisés lorsque tous les exemples de la base d'apprentissage sont indépendants les uns des autres et lorsque le temps n'est pas un paramètre fonctionnel.

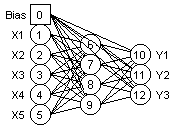
RESEAUX STATIQUES MULTI-SORTIES

Le graphique ci-contre représente le premier type de réseaux multi-sorties où toutes les sorties sont une combinaison linéaire des neurones de la couche cachée.

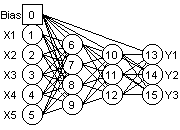
RESEAUX STATIQUES MULTI-COUCHES

Les réseaux multi-couches (et ici également multi-sorties) sont inutiles en régression mais peuvent s'avérer utiles en classification.
Nécessite Neuro One Expert.

RESEAUX STATIQUES TOUS CONNECTES

Ces réseaux se caractérisent par leurs neurones cachés qui dépendent les uns des autres. Ils sont très peu employés.

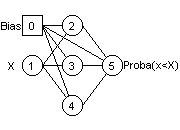
RESEAUX DE PROBABILITE

Les réseaux de neurones sont d'excellents outils pour caractériser la fonction de répartition empirique et la fonction de densité d'une loi de probabilité quelconque. Les résultats sont très bons pour les lois à queues épaisses et l'estimation des valeurs extrêmes.

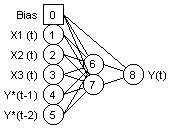
RESEAUX STATIQUES TEMPORELS

Pour ces réseaux qui restent encore des réseaux statiques, le temps est un paramètre fonctionnel important et on parle de séquence de données espacées à intervalles de temps constants. Les termes Y*(t-1) et Y*(t-2) sont les valeurs de sortie observées (ou mesurées) tandis que Y est la valeur de sortie calculée par le modèle.

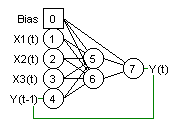
RESEAUX DYNAMIQUES ENTREES-SORTIES

Ces réseaux sont dynamiques car ils incorporent des bouclages. Le temps est un paramètre fonctionnel important. Les termes Y(t-1) et Y(t) sont les valeurs de sortie calculées par le modèle.

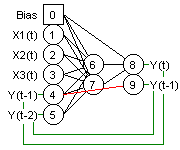
RESEAUX DYNAMIQUES MULTI-BOUCLES

Neuro One permet l'utilisation de plusieurs retards, ici 2, mais ce nombre n'est pas limité.

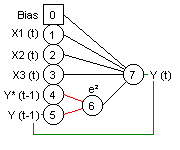
RESEAUX ARIMA/GARCH, etc...

Neuro One permet la construction de réseaux complexes, et notamment de réseaux ARIMA ou GARCH qui comparent valeurs observées et valeurs calculées.
Nécessite Neuro One Expert.

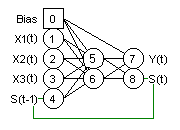
RESEAUX DYNAMIQUES D'ETATS

Le deuxième type de réseaux dynamiques. Les modèles d'états caractérisent les modèles à états internes non mesurables.

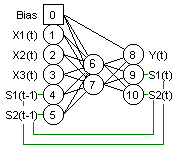
RESEAUX DYNAMIQUES MULTI-ETATS

Neuro One n'est pas limité dans le nombre d'états.